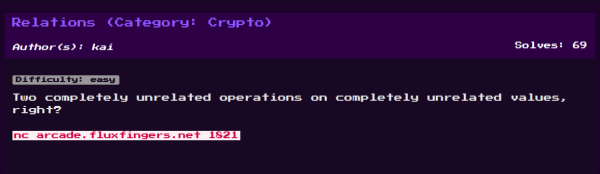
Hack.lu CTF is over and we (@teambi0s) finished 13th globally and since we were registered as a local team (thanks to @GeethnaTk) and stood first among the teams registered locally, hence we are eligible for prizes! Yay! This blog post covers detailed solutions to two of the crypto challenges from Hack.lu CTF 2018- Relations and... Continue Reading →
InCTF International 2018- Crypto Writeups [Part-2]
Intended solutions of two crypto challenges from InCTF International 2018: Request-Auth and EC-Auth
InCTF International 2018- Crypto Writeups [Part-1]
Write-ups of two crypto challenges from InCTF-2018: Throwback and Baby-Alice-Bob
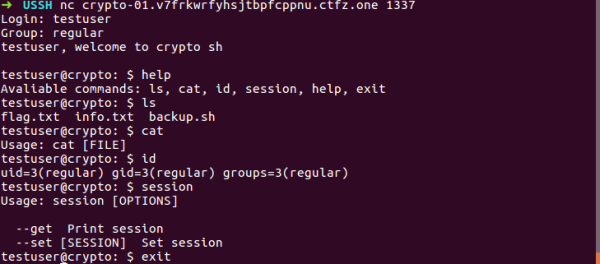
Exploiting cookie auth mechanism: CTFZone USSH-3.0 write-up
In this post, I will be discussing my solution for USSH-3.0 challenge from CTFZone which I think is the unintended way. The challenge was quite peculiar involving "blind" exploit as you will see in this write-up. Some parts of the challenge might look like guessing, but if you read this write-up start-to-end, you will see... Continue Reading →
ASIS CTF Quals 2018: Crypto Write-ups
Write-ups of 2 Crypto challenges from ASIS CTF Quals 2018- Uncle Sam(123 points) and OPEC (207 points)
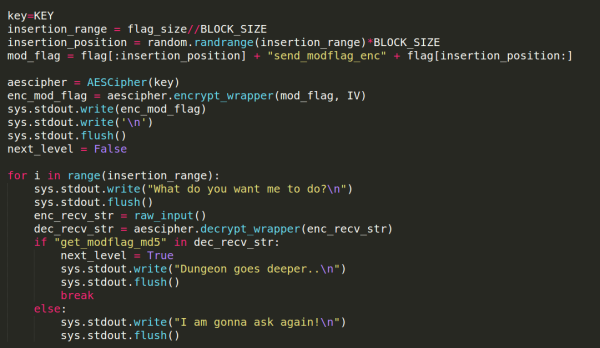
Swamp CTF 2018- Locked Dungeons-2 Write-up
CBC Bit Flipping Attack + Vulnerable unpadding function + Byte by Byte decryption
Pragyan CTF- RSA’s Quest
Points: 200 Description: Rivest comes up with an encryption, and Shamir creates a service for decrypting any cipher text encrypted using Rivests’s encryption. Adleman is asked to decrypt a specific ciphertext, but he is not able to do so directly through Shamir’s service. Help him out. This CTF had some okay-ish crypto challenges(didn't like the first... Continue Reading →
CNVService- AceBear CTF 2018 Writeup
This challenge was by far the most interesting and tricky Bit Flipping Attack I had come across, and I couldn't resist but share the write-up of this challenge. The challenge is one of the best illustrations of Bit Flipping Attack on Chained Block Cipher modes so, it is highly recommended for people who want to get... Continue Reading →
Rule86 – Insomni’hack Teaser 2018 Writeup
Points: 78 Description: Kevin is working on a new synchronous stream cipher, but he has been re-using his key. Although I could not solve the challenge completely during the CTF (I was stuck in the last stage), I liked the idea behind the last part of the exploit and so I am writing this post... Continue Reading →
DLP and Baby Step Giant Step Algorithm
Topics covered: Cyclic Groups Discrete Logarithm Problem Applications Attacks on DLP Brute Force Attack on DLP Baby Step Giant Step Algorithm CTF Challenges based on DLP Prerequisites: Mathematical Structures Cyclic Groups Abelian Groups in which all the elements can be produced using a single element in the group. This element is known as a generator... Continue Reading →